A revolution in knot theory
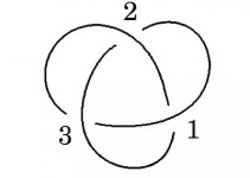
This knot has Gauss code O1U2O3U1O2U3.<br>Credit: Graphic by Sam Nelson<br><br>
This idea led Peter Guthrie Tait to prepare meticulous and quite beautiful tables of knots, in an effort to elucidate when two knots are truly different. From the point of view of physics, Kelvin and Tait were on the wrong track: the atomic viewpoint soon made the theory of ether obsolete. But from the mathematical viewpoint, a gold mine had been discovered: The branch of mathematics now known as “knot theory” has been burgeoning ever since.
In his article “The Combinatorial Revolution in Knot Theory”, to appear in the December 2011 issue of the Notices of the AMS,, Sam Nelson describes a novel approach to knot theory that has gained currency in the past several years and the mysterious new knot-like objects discovered in the process.
As sailors have long known, many different kinds of knots are possible; in fact, the variety is infinite. A *mathematical* knot can be imagined as a knotted circle: Think of a pretzel, which is a knotted circle of dough, or a rubber band, which is the “un-knot” because it is not knotted. Mathematicians study the patterns, symmetries, and asymmetries in knots and develop methods for distinguishing when two knots are truly different.
Mathematically, one thinks of the string out of which a knot is formed as being a one-dimensional object, and the knot itself lives in three-dimensional space. Drawings of knots, like the ones done by Tait, are projections of the knot onto a two-dimensional plane. In such drawings, it is customary to draw over-and-under crossings of the string as broken and unbroken lines. If three or more strands of the knot are on top of each other at single point, we can move the strands slightly without changing the knot so that every point on the plane sits below at most two strands of the knot. A planar knot diagram is a picture of a knot, drawn in a two-dimensional plane, in which every point of the diagram represents at most two points in the knot. Planar knot diagrams have long been used in mathematics as a way to represent and study knots.
As Nelson reports in his article, mathematicians have devised various ways to represent the information contained in knot diagrams. One example is the Gauss code, which is a sequence of letters and numbers wherein each crossing in the knot is assigned a number and the letter O or U, depending on whether the crossing goes over or under. The Gauss code for a simple knot might look like this: O1U2O3U1O2U3.
In the mid-1990s, mathematicians discovered something strange. There are Gauss codes for which it is impossible to draw planar knot diagrams but which nevertheless behave like knots in certain ways. In particular, those codes, which Nelson calls *nonplanar Gauss codes*, work perfectly well in certain formulas that are used to investigate properties of knots. Nelson writes: “A planar Gauss code always describes a [knot] in three-space; what kind of thing could a nonplanar Gauss code be describing?” As it turns out, there are “virtual knots” that have legitimate Gauss codes but do not correspond to knots in three-dimensional space. These virtual knots can be investigated by applying combinatorial techniques to knot diagrams.
Just as new horizons opened when people dared to consider what would happen if -1 had a square root—and thereby discovered complex numbers, which have since been thoroughly explored by mathematicians and have become ubiquitous in physics and engineering—mathematicians are finding that the equations they used to investigate regular knots give rise to a whole universe of “generalized knots” that have their own peculiar qualities. Although they seem esoteric at first, these generalized knots turn out to have interpretations as familiar objects in mathematics. “Moreover,” Nelson writes, “classical knot theory emerges as a special case of the new generalized knot theory.”
Related to this subject are an upcoming issue of the Journal of Knot Theory and its Ramifications, devoted to virtual knot theory, and the upcoming Knots in Washington conference at George Washington University, December 2-4, 2011, which will focus on on “Categorification of Knots, Algebras, and Quandles; Quantum Computing”.
Specific questions are best directed to the author, whose email address is given in the article. General questions can be directed to:
Mike Breen and Annette Emerson
AMS Public Awareness Office
Email: paoffice@ams.org
Telephone: 401-455-4000
Founded in 1888 to further mathematical research and scholarship, today the more than 30,000 member American Mathematical Society fulfills its mission through programs and services that promote mathematical research and its uses, strengthen mathematical education, and foster awareness and appreciation of mathematics and its connections to other disciplines and to everyday life.
American Mathematical Society
201 Charles Street
Providence, RI 02904
401-455-4000
Media Contact
More Information:
http://www.ams.orgAll latest news from the category: Science Education
Newest articles
High-energy-density aqueous battery based on halogen multi-electron transfer
Traditional non-aqueous lithium-ion batteries have a high energy density, but their safety is compromised due to the flammable organic electrolytes they utilize. Aqueous batteries use water as the solvent for…
First-ever combined heart pump and pig kidney transplant
…gives new hope to patient with terminal illness. Surgeons at NYU Langone Health performed the first-ever combined mechanical heart pump and gene-edited pig kidney transplant surgery in a 54-year-old woman…
Biophysics: Testing how well biomarkers work
LMU researchers have developed a method to determine how reliably target proteins can be labeled using super-resolution fluorescence microscopy. Modern microscopy techniques make it possible to examine the inner workings…





















