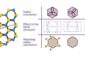
The poppy-seed bagel theorem

If you run into Ed Saff at a cocktail party and ask him what he does for a living, the mathematician is likely to reply that he is working on a “method for creating the perfect poppy-seed bagel.” Then he’ll pause and add, “Maybe that’s not the most accurate description, but it’s the most digestible.”
More accurately, Saff, who is a mathematics professor at Vanderbilt, has been working with his colleague Associate Professor of Mathematics Doug Hardin to come up with a new and improved way to distribute points uniformly on various types of surfaces. Plotting a large set of equidistant points on a flat surface doesn’t take a mathematician: Any draftsman can do it. Throw in a curve or two, however, and the problem gets much tougher. For complex surfaces like spheres and bagels (which form a shape that mathematicians call a torus), it becomes so hard, in fact, that mathematicians have not found a way to do it with absolute precision.
Recently, Hardin and Saff analyzed a method for generating large numbers of points that are spread with near uniformity over practically any surface of any dimension. Their effort is described in the cover article of the November issue of Notices of the American Mathematical Society.
The procedure has a surprising number of applications. Among other things, it comes in handy when trying to digitize curved surfaces for computer graphics and animations with greater efficiency, in placing the elements of a sonar net on the ocean bottom in the best locations to detect the presence of submarines, and in testing radar systems in aircraft to ensure uniform coverage.
The new results are built on Saff’s previous work in collaboration with A. B. J. Kuijlaars of Katholieke Universiteit Leuven, Belgium. It dealt with optimal designs of soccer-ball shaped objects called fullerenes, which are constructed from properly selected points on the surface of a sphere. Saff and Hardin have extended that work so that it is no longer limited to spherical surfaces, but now applies to elliptical, toroidal, saddle and other two-dimensional surfaces, as well as three-dimensional volumes. (They also handle surfaces with four or more dimensions, most of which don’t have known physical manifestations but are of importance in areas such as message coding.)
Hardin and Saff’s approach assumes that there is a repelling force acting between the points, and then, depending on the strength of the force, positions the points in the most energy-efficient manner (one that minimizes the total amount of energy in the system). For example, if the points strongly repel each other, then they tend to spread apart until there is as much distance between them as possible.
In particular, the mathematicians investigated equilibrium cases in which the repelling force between any pair of particles is inversely proportional to the distance between them raised to a power. Their formulation is a generalization of the inverse square law that is well known in physics, where it describes the behavior of forces such as electrical charge. In this case, however, the power depends on a parameter labeled “s.” Hardin and Saff have shown that when “s” is small, the points act as if they are responding to a long-range force, and when “s” is large, they act as if they are subject to a short-range force. (In these terms, the familiar forces of gravity and electromagnetism are long-range forces, while the strong force that binds the atomic nucleus together is a short-range force.)
“Think of a room full of people,” says Hardin. “In the short-range case, they act like fighting dictators and move until they are spread uniformly around the room. In the long-range case, however, they act as if they are afraid of crowds and end up lining the edge of the room.”
Such long-range/short-range behavior is illustrated by the distribution of points on the surface of a torus (a.k.a. bagel). In the case of a thousand points, when “s” is small, the points line up along the outer rim of the bagel and look something like the pattern of treads on a tire. As the value of “s” increases, however, the points spread out over more and more of the surface until they reach the stage where they are spread as uniformly as possible. As “s” increases beyond that critical value, however, the points may move about but the overall uniformity remains the same.
Hardin and Saff have also discovered – and rigorously justified – that this critical value of “s” is precisely equal to the dimension of the surface to which the points are restricted. In the case of the bagel, for example, using a value of “s” greater than or equal to two produces the most uniform distribution of seeds, resulting in the “nearly perfect” poppy-seed bagel. But using a value of “s” less than two will not spread the seeds evenly.
The insights that this model provides may be useful in creating new materials on the micron scale with novel physical and electrical properties. The mathematicians are collaborating with physicists Mark Bowick of Syracuse University and Alex Travesset at Iowa State University to explore this possibility. In particular, the researchers believe that an improved understanding of the relationship between certain chemical forces and surface shapes will allow them to create new kinds of thin films and self-assembling membranes which could be useful in certain medical applications.
“I think that we are really at the very beginning of something very big and very exciting that we couldn’t see when we looked only at the sphere,” says Saff.
“Now, if we could only figure out how to design the perfect cheese danish!”
Media Contact
More Information:
http://www.vanderbilt.eduAll latest news from the category: Physics and Astronomy
This area deals with the fundamental laws and building blocks of nature and how they interact, the properties and the behavior of matter, and research into space and time and their structures.
innovations-report provides in-depth reports and articles on subjects such as astrophysics, laser technologies, nuclear, quantum, particle and solid-state physics, nanotechnologies, planetary research and findings (Mars, Venus) and developments related to the Hubble Telescope.
Newest articles

A universal framework for spatial biology
SpatialData is a freely accessible tool to unify and integrate data from different omics technologies accounting for spatial information, which can provide holistic insights into health and disease. Biological processes…

How complex biological processes arise
A $20 million grant from the U.S. National Science Foundation (NSF) will support the establishment and operation of the National Synthesis Center for Emergence in the Molecular and Cellular Sciences (NCEMS) at…
Airborne single-photon lidar system achieves high-resolution 3D imaging
Compact, low-power system opens doors for photon-efficient drone and satellite-based environmental monitoring and mapping. Researchers have developed a compact and lightweight single-photon airborne lidar system that can acquire high-resolution 3D…