A pre-crack might propagate or stick under mechanical and electrical loading
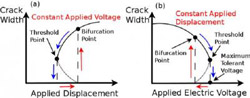
This is a schematic illustration of the hysteresis loops of a crack width versus (a) the applied displacement under a constant applied electric voltage, and (b) the applied electric voltage under a constant applied displacement.<br><br>Credit: ©Science China Press<br>
Professor ZHANG Tong-Yi and his student, Mr. Tao Xie, from the Department of Mechanical Engineering, Hong Kong University of Science and Technology, found that the two problems are switchable, depending on the loading conditions, sample geometries and material properties. Based on his 20-year research experience on the fracture of dielectric and piezoelectric ceramics, Prof. ZHANG developed a novel pre-cracked parallel-plate capacitor model to analytically investigate the role of electrostatic tractions in fracture and electric sticking behaviors.
“Prof. ZHANG and Mr. Tao Xie provided a new fracture criterion based on the energy release rate and crack opening. Their work, entitled “Effect of electrostatic tractions on the fracture behavior of a dielectric material under mechanical and/or electric loading”, was published in SCIENCE CHINA Technological Sciences, 2012.
Dielectric and piezoelectric ceramics are important materials for a wide variety of applications in electronic, microelectronic, and mechatronic devices and micro/nanoelectromechanical systems because of their pronounced dielectric, piezoelectric, and pyroelectric properties. However, these materials are brittle and susceptible to cracking. They may include various defects, such as dislocations, electric domain walls, grain boundaries, flaws, pores, impurities and inclusions. The defects induce local stress and/or electric field concentrations, which may consequently cause crack initiation, crack growth, and partial discharge, leading to dielectric breakdown, fracture, and failure. Because of the importance of the reliability of these devices, there has been tremendous interest in studying the fracture and failure behaviors of such materials. The traction-free (i.e., zero mechanical surface force) boundary condition has been commonly adopted in analyzing the fracture of dielectric and piezoelectric ceramics, which ignores completely electrostatic tractions.
However, induced charges appear along crack faces of an electrically insulating crack when the dielectric constant of the crack interior differs from that of the material, thereby producing electrostatic tractions along the crack faces. The electrostatic tractions will cause the two crack faces to stick together if they are strong enough.
This is a typical coupling problem between mechanical and electrical fields, for which it is a great challenge to obtain an analytic solution. Therefore, developing a simple and ideal model, which allows one to carry out an analytic study of the fracture and electric sticking problems, is fundamentally important in capturing the essential features of the fracture and/or electric sticking behaviors and to provide fracture criteria. A pre-cracked parallel capacitor model was thus developed with rigid electrodes adhered to the two surfaces of the capacitor. The capacitor was an infinitely large plate with a semi-infinite long preexisting crack of finite thickness, loaded by mechanical displacement and electric voltage. With this model, the energy release rate for crack propagation can be easily derived analytically without calculating the complex stress and electric fields near the crack tip. Electric sticking of the two crack faces occurs when the crack-closing displacement driven by the electrostatic tractions is equal to or larger than the original crack width.
Although linear constitutive equations are employed to describe material behaviors in the mechanical and electric fields, electrostatic tractions make the capacitor behave nonlinearly, as shown in the above figure for the bifurcation phenomenon of crack opening. Under an applied electric voltage, there is bifurcation behavior between bifurcation and threshold applied displacements (Figure (a)). When the applied displacement is lower than the bifurcation displacement, there are two solutions for the crack opening displacement and the bifurcation behavior occurs until the applied displacement is decreased to the threshold. When the applied displacement is lower than the threshold, there is no physically meaningful solution for the crack opening displacement. The bifurcation behavior yields a hysteresis loop of crack displacement versus applied displacement (Figure (a)).
When the applied displacement is decreased from high values, the crack opening displacement will smoothly pass the bifurcation point and decrease to the threshold point, at which the crack opening displacement will drop from a finite value to zero. When the applied displacement is lower than the threshold, the crack is closed so the upper and lower crack faces stick together. In an experiment, if an electric voltage is applied first and then the mechanical displacement, the crack will not open until the applied displacement reaches the bifurcation value. At the bifurcation displacement, the crack suddenly opens and the crack opening displacement jumps from zero to another finite value. The bifurcation and threshold displacements both depend on the applied electric voltage and the ratio of the dielectric constants, implying that the electrostatic tractions play a critical role. Under a given mechanical displacement, the crack opening displacement will decrease with increasing applied electric voltage until crack closure (Figure (b)), at which the electric voltage is called the maximum tolerated voltage , the conjugate of the threshold displacement. There is bifurcation behavior between the maximum tolerated voltage and the bifurcation voltage, conjugate of the bifurcation displacement. If the applied electric voltage exceeds the maximum tolerated voltage, the crack will close and the fracture problem is then converted to an electric field-induced sticking problem. The crack width versus applied electric voltage under a given mechanical displacement also shows a hysteresis loop (Figure (b)). In an experiment, if a sustained mechanical displacement is applied first, and then the applied electric voltage is increased from zero, the crack width will decrease smoothly with increasing electric voltage, passing the bifurcation point, until reaching the maximum tolerated voltage, at which the crack width drops from a finite value to zero. Afterward, increasing the electric voltage will result in the two crack faces sticking together more tightly. When the electric voltage is decreased from a value higher than the maximum tolerated voltage, the crack will not open until the electric voltage is decreased to the bifurcation point, at which the crack opens suddenly and the crack width jumps from zero to another finite value.
An analytic formula of the failure criterion was derived according to the energy release rate. The results show that an applied electric field impedes crack propagation while an applied mechanical load tends to propagate the crack. The applied electric field will play a more significant role in the fracture behavior, if the material dielectric constant is higher and/or the mechanical fracture toughness of the material in terms of the critical energy release rate is lower. In an experiment on the fracture of a dielectric material under combined mechanical and electric loading, an electric field is usually applied first; a mechanical load is then applied and increased until fracture occurs. This is because increasing an applied electric field while maintaining a sustained mechanical load cannot fracture the tested samples. The pre-applied electric field may cause the crack faces to stick together. In this case, the applied displacement must be higher than the bifurcation displacement to open the crack; thus, the condition that the critical applied displacement for crack propagation must be larger than the bifurcation displacement should be an additional criterion for crack propagation.
See the article: Zhang Tong-Yi and Tao Xie. Effect of electrostatic tractions on the fracture behavior of a dielectric material under mechanical and/or electric loading. SCIENCE CHINA Technological Sciences. 2012
Media Contact
More Information:
http://zh.scichina.com/All latest news from the category: Materials Sciences
Materials management deals with the research, development, manufacturing and processing of raw and industrial materials. Key aspects here are biological and medical issues, which play an increasingly important role in this field.
innovations-report offers in-depth articles related to the development and application of materials and the structure and properties of new materials.
Newest articles

Why getting in touch with our ‘gerbil brain’ could help machines listen better
Macquarie University researchers have debunked a 75-year-old theory about how humans determine where sounds are coming from, and it could unlock the secret to creating a next generation of more…

Attosecond core-level spectroscopy reveals real-time molecular dynamics
Chemical reactions are complex mechanisms. Many different dynamical processes are involved, affecting both the electrons and the nucleus of the present atoms. Very often the strongly coupled electron and nuclear…
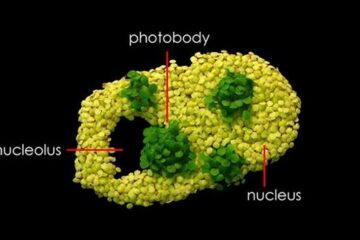
Free-forming organelles help plants adapt to climate change
Scientists uncover how plants “see” shades of light, temperature. Plants’ ability to sense light and temperature, and their ability to adapt to climate change, hinges on free-forming structures in their…