Blurred lines – mathematical software unites theory and practice
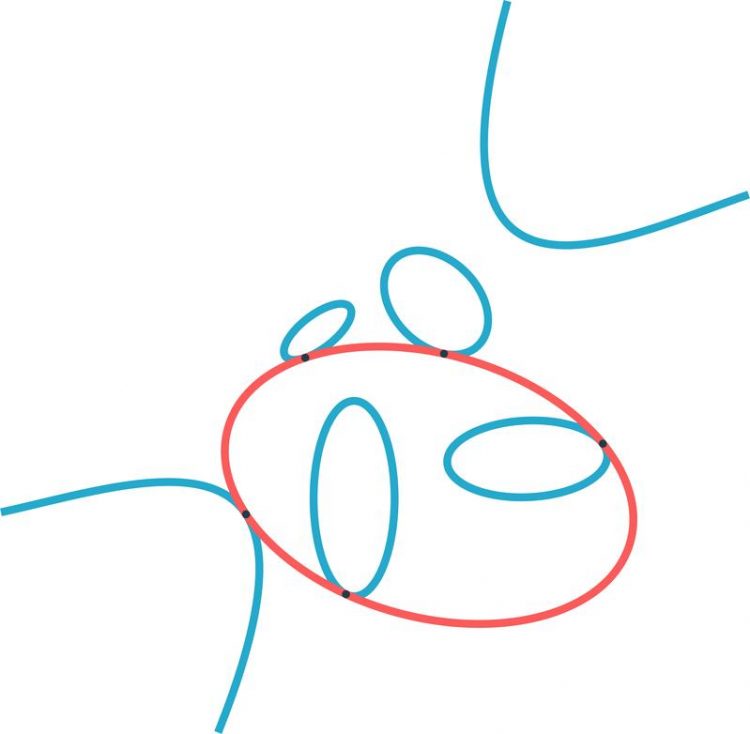
The figure illustrates a red ellipse that is tangent to four blue ellipses and one blue hyperbola. © Thomas Endler, MPI for Mathematics in the Sciences
The article “3264 Conics in a Second” exemplifies how mathematical software can serve as a bridge between theoretical problems and applied methods. Besides creating the extensive numerical software package “HomotopyContinuation.jl”, the authors also established an easily accessible website, which vividly showcases the various applications of the software.
One of these applications, in turn, constitutes the solution to a classical geometric problem, which was made even more accessible with a webapp.
Steiner's conic problem
The published paper revolves around a classical geometric problem from the perspective of modern numerical algorithms. In 1848 the mathematician Jakob Steiner posed the question of finding the number of conics tangent to five given conics.
A conic is a planar curve given by the intersection of the surface of a cone with a plane, yet it also constitutes the zero set of a quadratic equation in two variables. Even though Steiner's question initially seems quite academically rigorous in nature it is pertinent to modern applications. The conic problem is regarded as the origin of modern intersection theory.
This theory then forms the foundation for modern algorithms to compute the roots of polynomial systems, which is a fundamental problem in many applied fields: robotics, material sciences, machine learning, biology or dynamical systems theory are just a few exemplary fields, where polynomial equations need to be solved.
Software package HomotopyContinuation.jl
Exactly these numerical computations form the basis of the authors specialized software package HomotopyContinuation.jl, which was developed for Julia, a dynamic programming language focused on high-performance numerical analysis.
The accompanying website not only offers an all-encompassing software manual, but also contextualizes the software through an assortment of applications ranging from computer vision, robotics, chemistry, mathematics of data and algebraic geometry.
A variety of guides introduce the user to the software features and explain how they can be applied to numerous problems. Such as Steiner's conic problem, which can be formulated as a problem of finding the roots of a polynomial system. The customized software package is able to compute these solutions within a mere second.
The scientists at the Max Planck Institute and the Technical University of Berlin created a web interface accompanying their publication which allows the reader to easily compute the 3264 solutions for their chosen conics (see juliahomotopycontinuation.org/diy).
This innovative form of science communication is a novelty for publications in the Notices. The authors were able to use their software to compute exact equations for arrangements with real solutions to Steiner's conic problem.
Thus, they strikingly demonstrated how theoretical results involve numerical procedures, as well as the possible application of numerical methods in proofs of specific theoretical results.
Dr. Paul Breiding
Technical University of Berlin
Institute of Mathematics
Mail: p.breiding@tu-berlin.de
http://www.math.tu-berlin.de/~breiding
“3264 Conics in a Second” in the Notices of the American Mathematical Society
http://www.ams.org/journals/notices/202001/rnoti-p30.pdf
DOI: https://doi.org/10.1090/noti2010
http://www.juliahomotopycontinuation.org Information regarding the software HomotopyContinuation.jl
Media Contact
All latest news from the category: Information Technology
Here you can find a summary of innovations in the fields of information and data processing and up-to-date developments on IT equipment and hardware.
This area covers topics such as IT services, IT architectures, IT management and telecommunications.
Newest articles
Machine learning algorithm reveals long-theorized glass phase in crystal
Scientists have found evidence of an elusive, glassy phase of matter that emerges when a crystal’s perfect internal pattern is disrupted. X-ray technology and machine learning converge to shed light…

Mapping plant functional diversity from space
HKU ecologists revolutionize ecosystem monitoring with novel field-satellite integration. An international team of researchers, led by Professor Jin WU from the School of Biological Sciences at The University of Hong…

Inverters with constant full load capability
…enable an increase in the performance of electric drives. Overheating components significantly limit the performance of drivetrains in electric vehicles. Inverters in particular are subject to a high thermal load,…





















