Proof by Computer

These computer tools, based on the notion of “formal proof”, have in recent years been used to provide nearly infallible proofs of many important results in mathematics.
A ground-breaking collection of four articles by leading experts, published today in the Notices of the American Mathematical SocietyNotices of the American Mathematical Society (http://www.ams.org/notices), explores new developments in the use of formal proof in mathematics.
When mathematicians prove theorems in the traditional way, they present the argument in narrative form. They assume previous results, they gloss over details they think other experts will understand, they take shortcuts to make the presentation less tedious, they appeal to intuition, etc. The correctness of the arguments is determined by the scrutiny of other mathematicians, in informal discussions, in lectures, or in journals. It is sobering to realize that the means by which mathematical results are verified is essentially a social process and is thus fallible. When it comes to central, well known results, the proofs are especially well checked and errors are eventually found.
Nevertheless the history of mathematics has many stories about false results that went undetected for a long time. In addition, in some recent cases, important theorems have required such long and complicated proofs that very few people have the time, energy, and necessary background to check through them. And some proofs contain extensive computer code to, for example, check a lot of cases that would be infeasible to check by hand. How can mathematicians be sure that such proofs are reliable?
To get around these problems, computer scientists and mathematicians began to develop the field of formal proof. A formal proof is one in which every logical inference has been checked all the way back to the fundamental axioms of mathematics. Mathematicians do not usually write formal proofs because such proofs are so long and cumbersome that it would be impossible to have them checked by human mathematicians. But now one can get “computer proof assistants” to do the checking. In recent years, computer proof assistants have become powerful enough to handle difficult proofs.
Only in simple cases can one feed a statement to a computer proof assistant and expect it to hand over a proof. Rather, the mathematician has to know how to prove the statement; the proof then is greatly expanded into the special syntax of formal proof, with every step spelled out, and it is this formal proof that the computer checks. It is also possible to let computers loose to explore mathematics on their own, and in some cases they have come up with interesting conjectures that went unnoticed by mathematicians. We may be close to seeing how computers, rather than humans, would do mathematics.
The four Notices articles explore the current state of the art of formal proof and provide practical guidance for using computer proof assistants. If the use of these assistants becomes widespread, they could change deeply mathematics as it is currently practiced. One long-term dream is to have formal proofs of all of the central theorems in mathematics. Thomas Hales, one of the authors writing in the Notices, says that such a collection of proofs would be akin to “the sequencing of the mathematical genome”.
The four articles are:
Formal Proof, by Thomas Hales, University of Pittsburgh
Formal Proof—Theory and Practice, by John Harrison, Intel Corporation
Formal proof—The Four Colour Theorem, by Georges Gonthier, Microsoft
Research, Cambridge, England
Formal Proof—Getting Started, by Freek Wiedijk, Radboud University,
Nijmegen, Netherlands
The articles appear today in the December 2008 issue of the Notices
and are freely available at http://www.ams.org/notices.
Founded in 1888 to further mathematical research and scholarship, today the American Mathematical Society has more than 32,000 members. The Society fulfills its mission through programs and services that promote mathematical research and its uses, strengthen mathematical education, and foster awareness and appreciation of mathematics and its connections to other disciplines and to everyday life.
Media Contact
All latest news from the category: Information Technology
Here you can find a summary of innovations in the fields of information and data processing and up-to-date developments on IT equipment and hardware.
This area covers topics such as IT services, IT architectures, IT management and telecommunications.
Newest articles
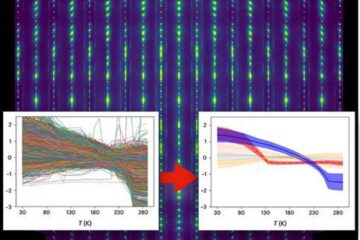
Machine learning algorithm reveals long-theorized glass phase in crystal
Scientists have found evidence of an elusive, glassy phase of matter that emerges when a crystal’s perfect internal pattern is disrupted. X-ray technology and machine learning converge to shed light…

Mapping plant functional diversity from space
HKU ecologists revolutionize ecosystem monitoring with novel field-satellite integration. An international team of researchers, led by Professor Jin WU from the School of Biological Sciences at The University of Hong…

Inverters with constant full load capability
…enable an increase in the performance of electric drives. Overheating components significantly limit the performance of drivetrains in electric vehicles. Inverters in particular are subject to a high thermal load,…





















